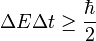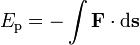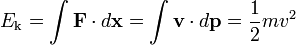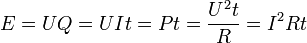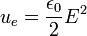Hello everyone i will not be blogging for a couple of days please bear with me.
science plus
basically for the science guys.
Saturday, June 25, 2011
urine therapy

“AUT (auto-urine therapy) is an ancient practice as it finds mention in many old texts of India such as Shivambhu Kalpa Vidhi and Damar Tantra. Shivambhu literally means water of Lord Shiva, a Hindu God. Urine therapists often speak of drinking Shivambhu, which means drinking the water of auspiciousness.”LifePositive.com
By: Eric Cho
You’d never think there was anything good in a pot of pee, right? Here’s news for you.
The use of urine for medicinal purposes can be traced to societies in ancient Egypt, China, Hindu and Aztec histories. Advocates also cite a prominent verse in the Bible: “Drink water from thine own cistern and the streams of thine own well.”
Urine therapy is also known as amaroli and it is an integral part of the Ayurvedic tradition of Yoga. Yogis who follow Ayurveda are advised to drink the urine they excrete between 4 and 6 in the morning because the hormones released are propitious in inducing the meditative state of mind.
The rationale behind urine therapy is quite simple and persuasive. Urine is believed to be a byproduct of blood filtration. It is NOT excess water that is released by the body. When blood filled with nutrients pass through the liver, the toxins are filtered out and are excreted as solid waste. The purified blood then travels to the kidney where excess nutrients are eliminated from the body. The medical name of urine is Plasma Ultrafiltrate. 95% of this liquid is water and the rest is a mixture of nutrients, urea, minerals, enzymes, antibodies and hormones.
Urine consists of urea, which is an antifungal, antibacterial and antiviral agent. Urea is produced when the body tries to balance the ratio of sodium chloride with water. Because of its ability to kill bacteria and limit inflammation, urea is often used in ointments and lotions.
Urine can be used internally or applied externally. For internal use, it is necessary to collect the morning’s first sample. A sterile container is used, and with a dropper the patient places anywhere between 5-10 drops under his tongue. The usual system is to use 1-5 drops on the first day, followed by 5-10 drops on the second day, 5-10 drops on the morning of the third day and 5-10 drops on the evening of the third day.
“Drinking urine is a good alternative wherever water is scarce. It not only satisfies the need for liquid, but also actually keeps the body healthy. Some time ago there was an earthquake in Egypt. A survivor was pulled out of the rubble in Cairo after being trapped for three days. The man had kept himself alive by, among other things, drinking his own urine and he was in excellent condition. I heard another story about a man who kept himself alive with his own urine for a week in a collapsed mine. At the time of his rescue, he looked fine and was in extraordinary health.” – Complete Guide to Urine Therapy Universal-Tao.com
Homeopathic urine therapy dilutes the urine with distilled water and this diluted solution is placed under the tongue till there is a reduction in symptoms.
Precautions are taken to ensure the purity and quality of the urine. The first urine of the day and the mid-stream urine is the best sample. Before collecting the sample, it is necessary to wash the genital area thoroughly. After taking the urine into the body, individuals should refrain from eating anything for at least half an hour.
For external application, new or old urine can be used. Since older urine has a higher concentration of ammonia, it is more effective against skin diseases and rashes. To make the urine old, it should be stored in a dark bottle and closed tightly and kept away from the sun for 3-4 days. A small amount of the solution is applied directly on the skin. It can also be sprayed on the skin or added to skin lotions, cream or moisturizers. Doctors advise against the use of soap immediately after applying urine on the skin.
Urine should never be injected into the body. Since urine therapy depends on the gradual introduction of urine into the body, a sudden introduction of urine into the bloodstream can cause damage.
Urine therapy is supposed to cure a variety of ailments ranging from Arthritis, Cancer, Hepatitis, Multiple Sclerosis, Eczema, Psoriasis, Diabetes, Herpes and adrenal failure. It is commonly used to combat venom from snakebites, jellyfish and beestings. Urine is the main ingredient in infertility drugs.
So, now you know there’s more to pee than what meets the eye!
“The medical community has already been aware of [urine's] astounding efficacy for decades, and yet none of us has ever been told about it. Why? Maybe they think it’s too controversial. Or maybe, more accurately, there wasn’t any monetary reward for telling people what scientists know about one of the most extraordinary natural healing elements in the world.” (Urine Therapy) – Shirley’s Wellness Cafe
Alternative Holistic Medicine
Amazon Books on Urine Therapy:
Uropathy
Your Own Perfect Medicine
The Golden Fountain: The Complete Guide to Urine Therapy
Urine Therapy: Nature’s Elixer for Good Health
Water of Life
Benefits of Moringa leaf
According to the annals of the ayurveda, India’s old tradition of medicines, the leaves of the Moringa Tree could treat at least 300 diseases.
Moringa leaf has no proven bad effects and is absolutely safe and organic. Because of its tolerant properties, it has been given to malnourished little babies in Africa. Athletes all over the world boost their performance abilities by taking huge quantities of the leaf to keep them fit both mentally and physically. It is their secret weapon. Even for senior citizens who are losing their sharpness of mind, the Moringa tree leaf could be a great help. In fact the powder is suitable for people from any age group.
The Moringa leaf is comparatively an unheard name in spite of the fact that it has been found mentioned more than two thousand years before, and the World Health Organization has been observing and utilizing the tree for more than forty years now as a cheap health supplement in the poverty-stricken countries the world over. There is a reason behind this. The selling of all kinds of health supplements, minerals and vitamins is a lucrative business. No big company would ever take the risk of introducing a name that could potentially harm and lower the sale of all other nutritional items. The same holds water for the pharmaceutical countries too. These huge companies would prefer to keep the general public in the dark about the benefits of the Moringa leaf to make big bucks for their own.
Written below are the benefits of the Moringa Leaf:
- Increases the Natural Defenses of the body
- Provides nourishment to the eyes and the brain.
- Promotes metabolism with bio-available ingredients
- Promotes the Cell structure of the body
- Promotes natural Serum cholesterol.
- Lowers the appearance of wrinkles and fine lines.
- Promotes the normal functioning of the liver and the kidney.
- Beautifies the skin
- Promotes energy
- Promotes proper digestion
- Acts as an antioxidant
- Takes care of the immune system of the body
- Promotes healthy circulatory system
- It is an anti-inflammatory
- Gives a feeling of general wellness
- Supports the normal sugar levels of the body.
 Moringa leaf boosts your energy in a natural manner, and is a remarkable source of nutrition. This energy promotion does not happen because of sugar, so it is lasts for a long time. Individuals ingesting it say that their ulcers are healed, tumors restricted, there are reduction in the arthritis pains and inflammations, controlled blood pressure, the skin problems are restored, and finally they have stronger defenses against diseases.
Moringa leaf boosts your energy in a natural manner, and is a remarkable source of nutrition. This energy promotion does not happen because of sugar, so it is lasts for a long time. Individuals ingesting it say that their ulcers are healed, tumors restricted, there are reduction in the arthritis pains and inflammations, controlled blood pressure, the skin problems are restored, and finally they have stronger defenses against diseases.Another property of the Moringa leaf is its soothing ability, because of which it can lower the blood pressure and promotes good sleep. It can also purify water since it has a detoxifying effect. Also a coagulant agent, Moringa can attach itself to hazardous bacteria and other materials, a process that is surmised to occur in the body too. The happy outcome is more sustained energy without any over-activity, balanced hormone and gland system, controlled blood pressure, and a rested nervous system.
Thursday, March 3, 2011
organic chemistry
Organic chemistry is a subdiscipline within chemistry involving the scientific study of the structure, properties, composition, reactions, and preparation (by synthesis or by other means) of carbon-based compounds, hydrocarbons, and their derivatives. These compounds may contain any number of other elements, including hydrogen, nitrogen, oxygen, the halogens as well as phosphorus, silicon and sulfur.[1][2][3]
Organic compounds are structurally diverse. The range of application of organic compounds is enormous. They either form the basis of or are important constituents of many products including plastics, drugs, petrochemicals, food, explosives, and paints. They form the basis of all earthly ln the early nineteenth century, chemists generally believed that compounds obtained from living organisms were too complex to be obtained synthetically. According to the concept of vitalism, organic matter was endowed with a "vital force". They named these compounds "organic" and directed their investigations toward inorganic materials that seemed more easily studied.[citation needed]
During the first half of the nineteenth century, scientists realized that organic compounds can be synthesized in the laboratory. Around 1816 Michel Chevreul started a study of soaps made from various fats and alkalis. He separated the different acids that, in combination with the alkali, produced the soap. Since these were all individual compounds, he demonstrated that it was possible to make a chemical change in various fats (which traditionally come from organic sources), producing new compounds, without "vital force". In 1828 Friedrich Wöhler produced the organic chemical urea (carbamide), a constituent of urine, from the inorganic ammonium cyanate NH4CNO, in what is now called the Wöhler synthesis. Although Wöhler was always cautious about claiming that he had disproved the theory of vital force, this event has often been thought of as a turning point.
In 1856 William Henry Perkin, while trying to manufacture quinine, accidentally manufactured the organic dye now known as Perkin's mauve. Through its great financial success, this discovery greatly increased interest in organic chemistry.
The crucial breakthrough for organic chemistry was the concept of chemical structure, developed independently and simultaneously by Friedrich August Kekule and Archibald Scott Couper in 1858. Both men suggested that tetravalent carbon atoms could link to each other to form a carbon lattice, and that the detailed patterns of atomic bonding could be discerned by skillful interpretations of appropriate chemical reactions.
The history of organic chemistry continued with the discovery of petroleum and its separation into fractions according to boiling ranges. The conversion of different compound types or individual compounds by various chemical processes created the petroleum chemistry leading to the birth of the petrochemical industry, which successfully manufactured artificial rubbers, the various organic adhesives, the property-modifying petroleum additives, and plastics.
The pharmaceutical industry began in the last decade of the 19th century when acetylsalicylic acid (more commonly referred to as aspirin) manufacture was started in Germany by Bayer. The first time a drug was systematically improved was with arsphenamine (Salvarsan). Numerous derivatives of the dangerously toxic atoxyl were examined by Paul Ehrlich and his group, and the compound with best effectiveness and toxicity characteristics was selected for production.
Although early examples of organic reactions and applications were often serendipitous, the latter half of the 19th century witnessed highly systematic studies of organic compounds. Beginning in the 20th century, progress of organic chemistry allowed the synthesis of highly complex molecules via multistep procedures. Concurrently, polymers and enzymes were understood to be large organic molecules, and petroleum was shown to be of biological origin. The process of finding new synthesis routes for a given compound is called total synthesis. Total synthesis of complex natural compounds started with urea, increased in complexity to glucose and terpineol, and in 1907, total synthesis was commercialized the first time by Gustaf Komppa with camphor. Pharmaceutical benefits have been substantial, for example cholesterol-related compounds have opened ways to synthesis of complex human hormones and their modified derivatives. Since the start of the 20th century, complexity of total syntheses has been increasing, with examples such as lysergic acid and vitamin B12. Today's targets feature tens of stereogenic centers that must be synthesized correctly with asymmetric synthesis.
Biochemistry, the chemistry of living organisms, their structure and interactions in vitro and inside living systems, has only started in the 20th century, opening up a new chapter of organic chemistry with enormous scope. Biochemistry, like organic chemistry, primarily focuses on compounds containing carbon.
Organic compounds were traditionally characterized by a variety of chemical tests, called "wet methods," but such tests have been largely displaced by spectroscopic or other computer-intensive methods of analysis.[4] Listed in approximate order of utility, the chief analytical methods are:
Additional methods are described in the article on analytical chemistry.
Nonsystematic nomenclature is simpler and unambiguous, at least to organic chemists. Nonsystematic names do not indicate the structure of the compound. Nonsystematic names are common for complex molecules, which includes most natural products. Thus, the informally named lysergic acid diethylamide is systematically named (6aR,9R)-N,N-diethyl-7-methyl-4,6,6a,7,8,9-hexahydroindolo-[4,3-fg] quinoline-9-carboxamide.
With the increased use of computing, other naming methods have evolved that are intended to be interpreted by machines. Two popular formats are SMILES and InChI.
 The concept of functional groups is central in organic chemistry, both as a means to classify structures and for predicting properties. A functional group is a molecular module, and the reactivity of that functional group is assumed, within limits, to be the same in a variety of molecules. Functional groups can have decisive influence on the chemical and physical properties of organic compounds. Molecules are classified on the basis of their functional groups. Alcohols, for example, all have the subunit C-O-H. All alcohols tend to be somewhat hydrophilic, usually form esters, and usually can be converted to the corresponding halides. Most functional groups feature heteroatoms (atoms other than C and H). Organic compounds are classified according to functional groups, alcohols, carboxylic acids, amines, etc.
The concept of functional groups is central in organic chemistry, both as a means to classify structures and for predicting properties. A functional group is a molecular module, and the reactivity of that functional group is assumed, within limits, to be the same in a variety of molecules. Functional groups can have decisive influence on the chemical and physical properties of organic compounds. Molecules are classified on the basis of their functional groups. Alcohols, for example, all have the subunit C-O-H. All alcohols tend to be somewhat hydrophilic, usually form esters, and usually can be converted to the corresponding halides. Most functional groups feature heteroatoms (atoms other than C and H). Organic compounds are classified according to functional groups, alcohols, carboxylic acids, amines, etc.
Both saturated (alicyclic) compounds and unsaturated compounds exist as cyclic derivatives. The most stable rings contain five or six carbon atoms, but large rings (macrocycles) and smaller rings are common. The smallest cycloalkane family is the three-membered cyclopropane ((CH2)3). Saturated cyclic compounds contain single bonds only, whereas aromatic rings have an alternating (or conjugated) double bond. Cycloalkanes do not contain multiple bonds, whereas the cycloalkenes and the cycloalkynes do.
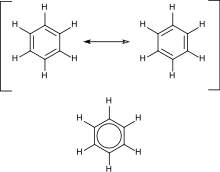 Aromatic hydrocarbons contain conjugated double bonds. The most important example is benzene, the structure of which was formulated by Kekulé who first proposed the delocalization or resonance principle for explaining its structure. For "conventional" cyclic compounds, aromaticity is conferred by the presence of 4n + 2 delocalized pi electrons, where n is an integer. Particular instability (antiaromaticity) is conferred by the presence of 4n conjugated pi electrons.
Aromatic hydrocarbons contain conjugated double bonds. The most important example is benzene, the structure of which was formulated by Kekulé who first proposed the delocalization or resonance principle for explaining its structure. For "conventional" cyclic compounds, aromaticity is conferred by the presence of 4n + 2 delocalized pi electrons, where n is an integer. Particular instability (antiaromaticity) is conferred by the presence of 4n conjugated pi electrons.
Examples of groups among the heterocyclics are the aniline dyes, the great majority of the compounds discussed in biochemistry such as alkaloids, many compounds related to vitamins, steroids, nucleic acids (e.g. DNA, RNA) and also numerous medicines. Heterocyclics with relatively simple structures are pyrrole (5-membered) and indole (6-membered carbon ring).
Rings can fuse with other rings on an edge to give polycyclic compounds. The purine nucleoside bases are notable polycyclic aromatic heterocycles. Rings can also fuse on a "corner" such that one atom (almost always carbon) has two bonds going to one ring and two to another. Such compounds are termed spiro and are important in a number of natural products.
 One important property of carbon is that it readily forms chain or even networks linked by carbon-carbon bonds. The linking process is called polymerization, and the chains or networks polymers, while the source compound is a monomer. Two main groups of polymers exist: those artificially manufactured are referred to as industrial polymers[5] or synthetic polymers and those naturally occurring as biopolymers.
One important property of carbon is that it readily forms chain or even networks linked by carbon-carbon bonds. The linking process is called polymerization, and the chains or networks polymers, while the source compound is a monomer. Two main groups of polymers exist: those artificially manufactured are referred to as industrial polymers[5] or synthetic polymers and those naturally occurring as biopolymers.
Since the invention of the first artificial polymer, bakelite, the family has quickly grown with the invention of others. Common synthetic organic polymers are polyethylene (polythene), polypropylene, nylon, teflon (PTFE), polystyrene, polyesters, polymethylmethacrylate (called perspex and plexiglas), and polyvinylchloride (PVC). Both synthetic and natural rubber are polymers.
The examples are generic terms, and many varieties of each of these may exist, with their physical characteristics fine tuned for a specific use. Changing the conditions of polymerisation changes the chemical composition of the product by altering chain length, or branching, or the tacticity. With a single monomer as a start the product is a homopolymer. Further, secondary component(s) may be added to create a heteropolymer (co-polymer) and the degree of clustering of the different components can also be controlled. Physical characteristics, such as hardness, density, mechanical or tensile strength, abrasion resistance, heat resistance, transparency, colour, etc. will depend on the final composition.
 Biomolecular chemistry is a major category within organic chemistry which is frequently studied by biochemists. Many complex multi-functional group molecules are important in living organisms. Some are long-chain biopolymers, and these include peptides, DNA, RNA and the polysaccharides such as starches in animals and celluloses in plants. The other main classes are amino acids (monomer building blocks of peptides and proteins), carbohydrates (which includes the polysaccharides), the nucleic acids (which include DNA and RNA as polymers), and the lipids. In addition, animal biochemistry contains many small molecule intermediates which assist in energy production through the Krebs cycle, and produces isoprene, the most common hydrocarbon in animals. Isoprenes in animals form the important steroid structural (cholesterol) and steroid hormone compounds; and in plants form terpenes, terpenoids, some alkaloids, and a unique set of hydrocarbons called biopolymer polyisoprenoids present in latex sap, which is the basis for making rubber.
Biomolecular chemistry is a major category within organic chemistry which is frequently studied by biochemists. Many complex multi-functional group molecules are important in living organisms. Some are long-chain biopolymers, and these include peptides, DNA, RNA and the polysaccharides such as starches in animals and celluloses in plants. The other main classes are amino acids (monomer building blocks of peptides and proteins), carbohydrates (which includes the polysaccharides), the nucleic acids (which include DNA and RNA as polymers), and the lipids. In addition, animal biochemistry contains many small molecule intermediates which assist in energy production through the Krebs cycle, and produces isoprene, the most common hydrocarbon in animals. Isoprenes in animals form the important steroid structural (cholesterol) and steroid hormone compounds; and in plants form terpenes, terpenoids, some alkaloids, and a unique set of hydrocarbons called biopolymer polyisoprenoids present in latex sap, which is the basis for making rubber.

 Synthetic organic chemistry is an applied science as it borders engineering, the "design, analysis, and/or construction of works for practical purposes". Organic synthesis of a novel compound is a problem solving task, where a synthesis is designed for a target molecule by selecting optimal reactions from optimal starting materials. Complex compounds can have tens of reaction steps that sequentially build the desired molecule. The synthesis proceeds by utilizing the reactivity of the functional groups in the molecule. For example, a carbonyl compound can be used as a nucleophile by converting it into an enolate, or as an electrophile; the combination of the two is called the aldol reaction. Designing practically useful syntheses always requires conducting the actual synthesis in the laboratory. The scientific practice of creating novel synthetic routes for complex molecules is called total synthesis.
Synthetic organic chemistry is an applied science as it borders engineering, the "design, analysis, and/or construction of works for practical purposes". Organic synthesis of a novel compound is a problem solving task, where a synthesis is designed for a target molecule by selecting optimal reactions from optimal starting materials. Complex compounds can have tens of reaction steps that sequentially build the desired molecule. The synthesis proceeds by utilizing the reactivity of the functional groups in the molecule. For example, a carbonyl compound can be used as a nucleophile by converting it into an enolate, or as an electrophile; the combination of the two is called the aldol reaction. Designing practically useful syntheses always requires conducting the actual synthesis in the laboratory. The scientific practice of creating novel synthetic routes for complex molecules is called total synthesis.
There are several strategies to design a synthesis. The modern method of retrosynthesis, developed by E.J. Corey, starts with the target molecule and splices it to pieces according to known reactions. The pieces, or the proposed precursors, receive the same treatment, until available and ideally inexpensive starting materials are reached. Then, the retrosynthesis is written in the opposite direction to give the synthesis. A "synthetic tree" can be constructed, because each compound and also each precursor has multiple syntheses.
The basic reaction types are: addition reactions, elimination reactions, substitution reactions, pericyclic reactions, rearrangement reactions and redox reactions. An example of a common reaction is a substitution reaction written as:
The number of possible organic reactions is basically infinite. However, certain general patterns are observed that can be used to describe many common or useful reactions. Each reaction has a stepwise reaction mechanism that explains how it happens in sequence—although the detailed description of steps is not always clear from a list of reactants alone.
The stepwise course of any given reaction mechanism can be represented using arrow pushing techniques in which curved arrows are used to track the movement of electrons as starting materials transition through intermediates to final products.
ife processes (with very few exceptions).
Organic compounds are structurally diverse. The range of application of organic compounds is enormous. They either form the basis of or are important constituents of many products including plastics, drugs, petrochemicals, food, explosives, and paints. They form the basis of all earthly ln the early nineteenth century, chemists generally believed that compounds obtained from living organisms were too complex to be obtained synthetically. According to the concept of vitalism, organic matter was endowed with a "vital force". They named these compounds "organic" and directed their investigations toward inorganic materials that seemed more easily studied.[citation needed]
During the first half of the nineteenth century, scientists realized that organic compounds can be synthesized in the laboratory. Around 1816 Michel Chevreul started a study of soaps made from various fats and alkalis. He separated the different acids that, in combination with the alkali, produced the soap. Since these were all individual compounds, he demonstrated that it was possible to make a chemical change in various fats (which traditionally come from organic sources), producing new compounds, without "vital force". In 1828 Friedrich Wöhler produced the organic chemical urea (carbamide), a constituent of urine, from the inorganic ammonium cyanate NH4CNO, in what is now called the Wöhler synthesis. Although Wöhler was always cautious about claiming that he had disproved the theory of vital force, this event has often been thought of as a turning point.
In 1856 William Henry Perkin, while trying to manufacture quinine, accidentally manufactured the organic dye now known as Perkin's mauve. Through its great financial success, this discovery greatly increased interest in organic chemistry.
The crucial breakthrough for organic chemistry was the concept of chemical structure, developed independently and simultaneously by Friedrich August Kekule and Archibald Scott Couper in 1858. Both men suggested that tetravalent carbon atoms could link to each other to form a carbon lattice, and that the detailed patterns of atomic bonding could be discerned by skillful interpretations of appropriate chemical reactions.
The history of organic chemistry continued with the discovery of petroleum and its separation into fractions according to boiling ranges. The conversion of different compound types or individual compounds by various chemical processes created the petroleum chemistry leading to the birth of the petrochemical industry, which successfully manufactured artificial rubbers, the various organic adhesives, the property-modifying petroleum additives, and plastics.
The pharmaceutical industry began in the last decade of the 19th century when acetylsalicylic acid (more commonly referred to as aspirin) manufacture was started in Germany by Bayer. The first time a drug was systematically improved was with arsphenamine (Salvarsan). Numerous derivatives of the dangerously toxic atoxyl were examined by Paul Ehrlich and his group, and the compound with best effectiveness and toxicity characteristics was selected for production.
Although early examples of organic reactions and applications were often serendipitous, the latter half of the 19th century witnessed highly systematic studies of organic compounds. Beginning in the 20th century, progress of organic chemistry allowed the synthesis of highly complex molecules via multistep procedures. Concurrently, polymers and enzymes were understood to be large organic molecules, and petroleum was shown to be of biological origin. The process of finding new synthesis routes for a given compound is called total synthesis. Total synthesis of complex natural compounds started with urea, increased in complexity to glucose and terpineol, and in 1907, total synthesis was commercialized the first time by Gustaf Komppa with camphor. Pharmaceutical benefits have been substantial, for example cholesterol-related compounds have opened ways to synthesis of complex human hormones and their modified derivatives. Since the start of the 20th century, complexity of total syntheses has been increasing, with examples such as lysergic acid and vitamin B12. Today's targets feature tens of stereogenic centers that must be synthesized correctly with asymmetric synthesis.
Biochemistry, the chemistry of living organisms, their structure and interactions in vitro and inside living systems, has only started in the 20th century, opening up a new chapter of organic chemistry with enormous scope. Biochemistry, like organic chemistry, primarily focuses on compounds containing carbon.
[edit] Characterization
Since organic compounds often exist as mixtures, a variety of techniques have also been developed to assess purity, especially important being chromatography techniques such as HPLC and gas chromatography. Traditional methods of separation include distillation, crystallization, and solvent extraction.Organic compounds were traditionally characterized by a variety of chemical tests, called "wet methods," but such tests have been largely displaced by spectroscopic or other computer-intensive methods of analysis.[4] Listed in approximate order of utility, the chief analytical methods are:
- Nuclear magnetic resonance (NMR) spectroscopy is the most commonly used technique, often permitting complete assignment of atom connectivity and even stereochemistry using correlation spectroscopy. The principal constituent atoms of organic chemistry - hydrogen and carbon - exist naturally with NMR-responsive isotopes, respectively 1H and 13C.
- Elemental analysis: A destructive method used to determine the elemental composition of a molecule. See also mass spectrometry, below.
- Mass spectrometry indicates the molecular weight of a compound and, from the fragmentation patterns, its structure. High resolution mass spectrometry can usually identify the exact formula of a compound and is used in lieu of elemental analysis. In former times, mass spectrometry was restricted to neutral molecules exhibiting some volatility, but advanced ionization techniques allow one to obtain the "mass spec" of virtually any organic compound.
- Crystallography is an unambiguous method for determining molecular geometry, the proviso being that single crystals of the material must be available and the crystal must be representative of the sample. Highly automated software allows a structure to be determined within hours of obtaining a suitable crystal.
Additional methods are described in the article on analytical chemistry.
[edit] Properties
Physical properties of organic compounds typically of interest include both quantitative and qualitative features. Quantitative information include melting point, boiling point, and index of refraction. Qualitative properties include odor, consistency, solubility, and color.[edit] Melting and boiling properties
In contrast to many inorganic materials, organic compounds typically melt and many boil. In earlier times, the melting point (m.p.) and boiling point (b.p.) provided crucial information on the purity and identity of organic compounds. The melting and boiling points correlate with the polarity of the molecules and their molecular weight. Some organic compounds, especially symmetrical ones, sublime, that is they evaporate without melting. A well known example of a sublimable organic compound is para-dichlorobenzene, the odiferous constituent of mothballs. Organic compounds are usually not very stable at temperatures above 300 °C, although some exceptions exist.[edit] Solubility
Neutral organic compounds tend to be hydrophobic, that is they are less soluble in water than in organic solvents. Exceptions include organic compounds that contain ionizable groups as well as low molecular weight alcohols, amines, and carboxylic acids where hydrogen bonding occurs. Organic compounds tend to dissolve in organic solvents. Solvents can be either pure substances like ether or ethyl alcohol, or mixtures, such as the paraffinic solvents such as the various petroleum ethers and white spirits, or the range of pure or mixed aromatic solvents obtained from petroleum or tar fractions by physical separation or by chemical conversion. Solubility in the different solvents depends upon the solvent type and on the functional groups if present.[edit] Solid state properties
Various specialized properties of molecular crystals and organic polymers with conjugated systems are of interest depending on applications, e.g. thermo-mechanical and electro-mechanical such as piezoelectricity, electrical conductivity (see conductive polymers and organic semiconductors), and electro-optical (e.g. non-linear optics) properties. For historical reasons, such properties are mainly the subjects of the areas of polymer science and materials science.[edit] Nomenclature
See also: IUPAC nomenclature
The names of organic compounds are either systematic, following logically from a set of rules, or nonsystematic, following various traditions. Systematic nomenclature is stipulated by specifications from IUPAC. Systematic nomenclature starts with the name for a parent structure within the molecule of interest. This parent name is then modified by prefixes, suffixes, and numbers to unambiguously convey the structure. Given that millions of organic compounds are known, rigorous use of systematic names can be cumbersome. Thus, IUPAC recommendations are more closely followed for simple compounds, but not complex molecules. To use the systematic naming, one must know the structures and names of the parent structures. Parent structures include unsubstituted hydrocarbons, heterocycles, and monofunctionalized derivatives thereof.Nonsystematic nomenclature is simpler and unambiguous, at least to organic chemists. Nonsystematic names do not indicate the structure of the compound. Nonsystematic names are common for complex molecules, which includes most natural products. Thus, the informally named lysergic acid diethylamide is systematically named (6aR,9R)-N,N-diethyl-7-methyl-4,6,6a,7,8,9-hexahydroindolo-[4,3-fg] quinoline-9-carboxamide.
With the increased use of computing, other naming methods have evolved that are intended to be interpreted by machines. Two popular formats are SMILES and InChI.
[edit] Structural drawings
Organic molecules are described more commonly by drawings or structural formulas, combinations of drawings and chemical symbols. The line-angle formula is simple and unambiguous. In this system, the endpoints and intersections of each line represent one carbon, and hydrogen atoms can either be notated explicitly or assumed to be present as implied by tetravalent carbon. The depiction of organic compounds with drawings is greatly simplified by the fact that carbon in almost all organic compounds has four bonds, oxygen two, hydrogen one, and nitrogen three.[edit] Classification of organic compounds
[edit] Functional groups
Main article: Functional group

The family of carboxylic acids contains a carboxyl (-COOH) functional group. Acetic acid is an example.
[edit] Aliphatic compounds
Main article: Aliphatic compound
The aliphatic hydrocarbons are subdivided into three groups of homologous series according to their state of saturation:- paraffins, which are alkanes without any double or triple bonds,
- olefins or alkenes which contain one or more double bonds, i.e. di-olefins (dienes) or poly-olefins.
- alkynes, which have one or more triple bonds.
Both saturated (alicyclic) compounds and unsaturated compounds exist as cyclic derivatives. The most stable rings contain five or six carbon atoms, but large rings (macrocycles) and smaller rings are common. The smallest cycloalkane family is the three-membered cyclopropane ((CH2)3). Saturated cyclic compounds contain single bonds only, whereas aromatic rings have an alternating (or conjugated) double bond. Cycloalkanes do not contain multiple bonds, whereas the cycloalkenes and the cycloalkynes do.
[edit] Aromatic compounds

Benzene is one of the best-known aromatic compounds as it is one of the simplest and most stable aromatics.
[edit] Heterocyclic compounds
Main article: Heterocyclic compound
The characteristics of the cyclic hydrocarbons are again altered if heteroatoms are present, which can exist as either substituents attached externally to the ring (exocyclic) or as a member of the ring itself (endocyclic). In the case of the latter, the ring is termed a heterocycle. Pyridine and furan are examples of aromatic heterocycles while piperidine and tetrahydrofuran are the corresponding alicyclic heterocycles. The heteroatom of heterocyclic molecules is generally oxygen, sulfur, or nitrogen, with the latter being particularly common in biochemical systems.Examples of groups among the heterocyclics are the aniline dyes, the great majority of the compounds discussed in biochemistry such as alkaloids, many compounds related to vitamins, steroids, nucleic acids (e.g. DNA, RNA) and also numerous medicines. Heterocyclics with relatively simple structures are pyrrole (5-membered) and indole (6-membered carbon ring).
Rings can fuse with other rings on an edge to give polycyclic compounds. The purine nucleoside bases are notable polycyclic aromatic heterocycles. Rings can also fuse on a "corner" such that one atom (almost always carbon) has two bonds going to one ring and two to another. Such compounds are termed spiro and are important in a number of natural products.
[edit] Polymers
Main article: Polymer

This swimming board is made of polystyrene, an example of a polymer.
Since the invention of the first artificial polymer, bakelite, the family has quickly grown with the invention of others. Common synthetic organic polymers are polyethylene (polythene), polypropylene, nylon, teflon (PTFE), polystyrene, polyesters, polymethylmethacrylate (called perspex and plexiglas), and polyvinylchloride (PVC). Both synthetic and natural rubber are polymers.
The examples are generic terms, and many varieties of each of these may exist, with their physical characteristics fine tuned for a specific use. Changing the conditions of polymerisation changes the chemical composition of the product by altering chain length, or branching, or the tacticity. With a single monomer as a start the product is a homopolymer. Further, secondary component(s) may be added to create a heteropolymer (co-polymer) and the degree of clustering of the different components can also be controlled. Physical characteristics, such as hardness, density, mechanical or tensile strength, abrasion resistance, heat resistance, transparency, colour, etc. will depend on the final composition.
[edit] Biomolecules

Maitotoxin, a complex organic biological toxin.
- Peptide Synthesis
-
- See also Peptide synthesis
- Oligonucleotide Synthesis
-
- See also Oligonucleotide synthesis
- Carbohydrate Synthesis
-
- See also Carbohydrate synthesis
[edit] Small molecules
In pharmacology, an important group of organic compounds is small molecules, also referred to as 'small organic compounds'. In this context, a small molecule is a small organic compound that is biologically active, but is not a polymer. In practice, small molecules have a molar mass less than approximately 1000 g/mol.
Molecular models of caffeine.
[edit] Fullerenes
Fullerenes and carbon nanotubes, carbon compounds with spheroidal and tubular structures, have stimulated much research into the related field of materials science.[edit] Others
Organic compounds containing bonds of carbon to nitrogen, oxygen and the halogens are not normally grouped separately. Others are sometimes put into major groups within organic chemistry and discussed under titles such as organosulfur chemistry, organometallic chemistry, organophosphorus chemistry and organosilicon chemistry.[edit] Organic synthesis

A synthesis designed by E.J. Corey for oseltamivir (Tamiflu). This synthesis has 11 distinct reactions.
There are several strategies to design a synthesis. The modern method of retrosynthesis, developed by E.J. Corey, starts with the target molecule and splices it to pieces according to known reactions. The pieces, or the proposed precursors, receive the same treatment, until available and ideally inexpensive starting materials are reached. Then, the retrosynthesis is written in the opposite direction to give the synthesis. A "synthetic tree" can be constructed, because each compound and also each precursor has multiple syntheses.
[edit] Organic reactions
Organic reactions are chemical reactions involving organic compounds. While pure hydrocarbons undergo certain limited classes of reactions, many more reactions which organic compounds undergo are largely determined by functional groups. The general theory of these reactions involves careful analysis of such properties as the electron affinity of key atoms, bond strengths and steric hindrance. These issues can determine the relative stability of short-lived reactive intermediates, which usually directly determine the path of the reaction.The basic reaction types are: addition reactions, elimination reactions, substitution reactions, pericyclic reactions, rearrangement reactions and redox reactions. An example of a common reaction is a substitution reaction written as:
- Nu− + C-X → C-Nu + X−
The number of possible organic reactions is basically infinite. However, certain general patterns are observed that can be used to describe many common or useful reactions. Each reaction has a stepwise reaction mechanism that explains how it happens in sequence—although the detailed description of steps is not always clear from a list of reactants alone.
The stepwise course of any given reaction mechanism can be represented using arrow pushing techniques in which curved arrows are used to track the movement of electrons as starting materials transition through intermediates to final products.
ife processes (with very few exceptions).
power cord
A power cord, line cord, or mains cable is a cord or cable that temporarily connects an electrical appliance to the distribution circuits of an electrical power source via a wall socket or extension cord.
The terms are generally used for cables using a power plug to connect to a single-phase alternating current power source at the local line voltage—(generally 100 to 240 volts, depending on the location). The terms power cable, mains lead or flex are also used. A lamp cord is a light weight ungrounded two wire cord used for small loads such as a table or floor lamp. The term cord set is also used to distinguish those cords that include connectors molded to the cord at each end.
Power cables may be either fixed or detachable from the appliance. In the case of detachable leads, the appliance end of the power cord has a socket rather than a plug to link it to the appliance, to avoid the dangers from having a live protruding pin. Cords may also have twist-locking features, or other attachments to prevent accidental disconnection at one or both ends. A cord set may include accessories such as fuses for overcurrent protection, a pilot lamp to indicate voltage is present, or a leakage current detector. Power cords for sensitive instruments, or audio/video equipment may also include a shield over the power conductors to minimize electromagnetic interference.
The terms are generally used for cables using a power plug to connect to a single-phase alternating current power source at the local line voltage—(generally 100 to 240 volts, depending on the location). The terms power cable, mains lead or flex are also used. A lamp cord is a light weight ungrounded two wire cord used for small loads such as a table or floor lamp. The term cord set is also used to distinguish those cords that include connectors molded to the cord at each end.
Power cables may be either fixed or detachable from the appliance. In the case of detachable leads, the appliance end of the power cord has a socket rather than a plug to link it to the appliance, to avoid the dangers from having a live protruding pin. Cords may also have twist-locking features, or other attachments to prevent accidental disconnection at one or both ends. A cord set may include accessories such as fuses for overcurrent protection, a pilot lamp to indicate voltage is present, or a leakage current detector. Power cords for sensitive instruments, or audio/video equipment may also include a shield over the power conductors to minimize electromagnetic interference.
Tuesday, March 1, 2011
energy
Energy
From Wikipedia, the free encyclopedia
This article is about the scalar physical quantity. For other uses, see Energy (disambiguation).

Lightning is the electric breakdown of air by strong electric fields, which produce a force on charges. When these charges move through a distance, a flow of energy occurs. The electric potential energy in the atmosphere then is transformed into thermal energy, light, and sound, which are other forms of energy.
In physics, energy (Greek: ἐνέργεια energeia "activity, operation"[1]) is a quantity that is often understood as the ability a physical system has to do work on other physical systems.[2][3] Since work is defined as a force acting through a distance (a length of space), energy is always equivalent to the ability to exert pulls or pushes against the basic forces of nature, along a path of a certain length.
The total energy contained in an object is identified with its mass, and energy (like mass), cannot be created or destroyed. When matter (ordinary material particles) is changed into energy (such as energy of motion, or into radiation), the mass of the system does not change through the transformation process. However, there may be mechanistic limits as to how much of the matter in an object may be changed into other types of energy and thus into work, on other systems. Energy, like mass, is ascalar physical quantity. In the International System of Units (SI), energy is measured in joules, but in many fields other units, such as kilowatt-hours andkilocalories, are customary. All of these units translate to units of work, which is always defined in terms of forces and the distances that the forces act through.
A system can transfer energy to another system by simply transferring matter to it (since matter is equivalent to energy, in accordance with its mass). However, when energy is transferred by means other than matter-transfer, the transfer produces changes in the second system, as a result of work done on it. This work manifests itself as the effect of force(s) applied through distances within the target system. For example, a system can emit energy to another by transferring (radiating) electromagnetic energy, but this creates forces upon the particles that absorb the radiation. Similarly, a system may transfer energy to another by physically impacting it, but that case the energy of motion in an object, called kinetic energy, results in forces acting over distances (new energy) to appear in another object that is struck. Transfer of thermal energy by heatoccurs by both of these mechanisms: heat can be transferred by electromagnetic radiation, or by physical contact in which which direct particle-particle impacts transfer kinetic energy.
Energy may be stored in systems without being present as matter, or as kinetic or electromagnetic energy. Stored energy is created whenever a particle has been moved through a field it interacts with (requiring a force to do so), but the energy to accomplish this is stored as a new position of the particles in the field-- a configuration that must be "held" or fixed by a different type of force (otherwise, the new configuration would resolve itself by the field pushing or pulling the particle back toward its previous position). This type of energy "stored" by force-fields and particles that have been forced into a new physical configuration in the field by doing work on them by another system, is referred to as potential energy. A simple example of potential energy is the work needed to lift an object in a gravity field, up to a support. Each of the basic forces of nature is associated with a different type of potential energy, and all types of potential energy (like all other types of energy) appears as system mass, whenever present. For example, a compressed spring will be slightly more massive than before it was compressed. Likewise, whenever energy is transferred between systems by any mechanism, an associated mass is transferred with it.
Any form of energy may be transformed into another form. For example, all types of potential energy are converted into kinetic energy when the objects are given freedom to move to different position (as for example, when an object falls off a support). When energy is in a form other than thermal energy, it may be transformed with good or even perfect efficiency, to any other type of energy, including electricity or production of new particles of matter. With thermal energy, however, there are often limits to the efficiency of the conversion to other forms of energy, as described by the second law of thermodynamics.
In all such energy transformation processes, the total energy remains the same, and a transfer of energy from one system to another, results in a loss to compensate for any gain. This principle, the conservation of energy, was first postulated in the early 19th century, and applies to any isolated system. According to Noether's theorem, the conservation of energy is a consequence of the fact that the laws of physics do not change over time.[4]
Although the total energy of a system does not change with time, its value may depend on the frame of reference. For example, a seated passenger in a moving airplane has zero kinetic energy relative to the airplane, but non-zero kinetic energy (and higher total energy) relative to the Earth.
Contents[hide] |
History
Main articles: History of energy and timeline of thermodynamics, statistical mechanics, and random processes
The word energy derives from the Greek ἐνέργεια energeia, which possibly appears for the first time in the work of Aristotle in the 4th century BC.
The concept of energy emerged out of the idea of vis viva (living force), which Gottfried Leibniz defined as the product of the mass of an object and its velocity squared; he believed that total vis viva was conserved. To account for slowing due to friction, Leibniz theorized that thermal energy consisted of the random motion of the constituent parts of matter, a view shared by Isaac Newton, although it would be more than a century until this was generally accepted. In 1807, Thomas Young was possibly the first to use the term "energy" instead of vis viva, in its modern sense.[5] Gustave-Gaspard Coriolis described "kinetic energy" in 1829 in its modern sense, and in 1853, William Rankine coined the term "potential energy". It was argued for some years whether energy was a substance (the caloric) or merely a physical quantity, such asmomentum.
William Thomson (Lord Kelvin) amalgamated all of these laws into the laws of thermodynamics, which aided in the rapid development of explanations of chemical processes by Rudolf Clausius, Josiah Willard Gibbs, and Walther Nernst. It also led to a mathematical formulation of the concept of entropy by Clausius and to the introduction of laws of radiant energy by Jožef Stefan.
During a 1961 lecture[6] for undergraduate students at the California Institute of Technology, Richard Feynman, a celebrated physics teacher and Nobel Laureate, said this about the concept of energy:
There is a fact, or if you wish, a law, governing all natural phenomena that are known to date. There is no known exception to this law—it is exact so far as we know. The law is called the conservation of energy. It states that there is a certain quantity, which we call energy, that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same.
Since 1918 it has been known that the law of conservation of energy is the direct mathematical consequence of the translational symmetry of the quantity conjugate to energy, namely time. That is, energy is conserved because the laws of physics do not distinguish between different instants of time (see Noether's theorem).
Energy in various contexts
The concept of energy and its transformations is useful in explaining and predicting most natural phenomena. The direction of transformations in energy (what kind of energy is transformed to what other kind) is often described by entropy (equal energy spread among all availabledegrees of freedom) considerations, as in practice all energy transformations are permitted on a small scale, but certain larger transformations are not permitted because it is statistically unlikely that energy or matter will randomly move into more concentrated forms or smaller spaces.
The concept of energy is widespread in all sciences.
- In the context of chemistry, energy is an attribute of a substance as a consequence of its atomic, molecular or aggregate structure. Since a chemical transformation is accompanied by a change in one or more of these kinds of structure, it is invariably accompanied by an increase or decrease of energy of the substances involved. Some energy is transferred between the surroundings and the reactants of the reaction in the form of heat or light; thus the products of a reaction may have more or less energy than the reactants. A reaction is said to be exergonic if the final state is lower on the energy scale than the initial state; in the case of endergonic reactions the situation is the reverse. Chemical reactions are invariably not possible unless the reactants surmount an energy barrier known as the activation energy. The speed of a chemical reaction (at given temperature T) is related to the activation energy E, by the Boltzmann's population factor e−E/kT – that is the probability of molecule to have energy greater than or equal to E at the given temperature T. This exponential dependence of a reaction rate on temperature is known as the Arrhenius equation.The activation energy necessary for a chemical reaction can be in the form of thermal energy.
- In biology, energy is an attribute of all biological systems from the biosphere to the smallest living organism. Within an organism it is responsible for growth and development of a biological cell or an organelle of a biological organism. Energy is thus often said to be stored by cells in the structures of molecules of substances such as carbohydrates (including sugars), lipids, and proteins, which release energy when reacted with oxygen in respiration. In human terms, the human equivalent (H-e) (Human energy conversion) indicates, for a given amount of energy expenditure, the relative quantity of energy needed for human metabolism, assuming an average human energy expenditure of 12,500kJ per day and a basal metabolic rate of 80 watts. For example, if our bodies run (on average) at 80 watts, then a light bulb running at 100 watts is running at 1.25 human equivalents (100 ÷ 80) i.e. 1.25 H-e. For a difficult task of only a few seconds' duration, a person can put out thousands of watts, many times the 746 watts in one official horsepower. For tasks lasting a few minutes, a fit human can generate perhaps 1,000 watts. For an activity that must be sustained for an hour, output drops to around 300; for an activity kept up all day, 150 watts is about the maximum.[7] The human equivalent assists understanding of energy flows in physical and biological systems by expressing energy units in human terms: it provides a “feel” for the use of a given amount of energy[8]
- In geology, continental drift, mountain ranges, volcanoes, and earthquakes are phenomena that can be explained in terms of energy transformations in the Earth's interior.,[9] while meteorological phenomena like wind, rain, hail, snow, lightning, tornadoes and hurricanes, are all a result of energy transformations brought about by solar energy on the atmosphere of the planet Earth.
- In cosmology and astronomy the phenomena of stars, nova, supernova, quasars and gamma ray bursts are the universe's highest-output energy transformations of matter. All stellar phenomena (including solar activity) are driven by various kinds of energy transformations. Energy in such transformations is either from gravitational collapse of matter (usually molecular hydrogen) into various classes of astronomical objects (stars, black holes, etc.), or from nuclear fusion (of lighter elements, primarily hydrogen).
Energy transformations in the universe over time are characterized by various kinds of potential energy that has been available since the Big Bang, later being "released" (transformed to more active types of energy such as kinetic or radiant energy), when a triggering mechanism is available.
Familiar examples of such processes include nuclear decay, in which energy is released that was originally "stored" in heavy isotopes (such as uranium and thorium), by nucleosynthesis, a process ultimately using the gravitational potential energy released from the gravitational collapse of supernovae, to store energy in the creation of these heavy elements before they were incorporated into the solar system and the Earth. This energy is triggered and released in nuclear fission bombs. In a slower process, radioactive decay of these atoms in the core of the Earth releases heat. This thermal energy drives plate tectonics and may lift mountains, via orogenesis. This slow lifting represents a kind of gravitational potential energy storage of the thermal energy, which may be later released to active kinetic energy in landslides, after a triggering event. Earthquakes also release stored elastic potential energy in rocks, a store that has been produced ultimately from the same radioactive heat sources. Thus, according to present understanding, familiar events such as landslides and earthquakes release energy that has been stored as potential energy in the Earth's gravitational field or elastic strain (mechanical potential energy) in rocks. Prior to this, they represent release of energy that has been stored in heavy atoms since the collapse of long-destroyed supernova stars created these atoms.
In another similar chain of transformations beginning at the dawn of the universe, nuclear fusion of hydrogen in the Sun also releases another store of potential energy which was created at the time of the Big Bang. At that time, according to theory, space expanded and the universe cooled too rapidly for hydrogen to completely fuse into heavier elements. This meant that hydrogen represents a store of potential energy that can be released by fusion. Such a fusion process is triggered by heat and pressure generated from gravitational collapse of hydrogen clouds when they produce stars, and some of the fusion energy is then transformed into sunlight. Such sunlight from our Sun may again be stored as gravitational potential energy after it strikes the Earth, as (for example) water evaporates from oceans and is deposited upon mountains (where, after being released at a hydroelectric dam, it can be used to drive turbines or generators to produce electricity). Sunlight also drives many weather phenomena, save those generated by volcanic events. An example of a solar-mediated weather event is a hurricane, which occurs when large unstable areas of warm ocean, heated over months, give up some of their thermal energy suddenly to power a few days of violent air movement. Sunlight is also captured by plants as chemical potential energy in photosynthesis, when carbon dioxide and water (two low-energy compounds) are converted into the high-energy compounds carbohydrates, lipids, and proteins. Plants also release oxygen during photosynthesis, which is utilized by living organisms as an electron acceptor, to release the energy of carbohydrates, lipids, and proteins. Release of the energy stored during photosynthesis as heat or light may be triggered suddenly by a spark, in a forest fire, or it may be made available more slowly for animal or human metabolism, when these molecules are ingested, andcatabolism is triggered by enzyme action.
Through all of these transformation chains, potential energy stored at the time of the Big Bang is later released by intermediate events, sometimes being stored in a number of ways over time between releases, as more active energy. In all these events, one kind of energy is converted to other types of energy, including heat.
Conservation of energy
Main article: Conservation of energy
Energy is subject to the law of conservation of energy. According to this law, energy can neither be created (produced) nor destroyed by itself. It can only be transformed.
Most kinds of energy (with gravitational energy being a notable exception)[10] are also subject to strict local conservation laws, as well. In this case, energy can only be exchanged between adjacent regions of space, and all observers agree as to the volumetric density of energy in any given space. There is also a global law of conservation of energy, stating that the total energy of the universe cannot change; this is a corollary of the local law, but not vice versa.[6][11] Conservation of energy is the mathematical consequence of translational symmetry of time(that is, the indistinguishability of time intervals taken at different time)[12] - see Noether's theorem.
According to energy conservation law the total inflow of energy into a system must equal the total outflow of energy from the system, plus the change in the energy contained within the system.
This law is a fundamental principle of physics. It follows from the translational symmetry of time, a property of most phenomena below the cosmic scale that makes them independent of their locations on the time coordinate. Put differently, yesterday, today, and tomorrow are physically indistinguishable.
This is because energy is the quantity which is canonical conjugate to time. This mathematical entanglement of energy and time also results in the uncertainty principle - it is impossible to define the exact amount of energy during any definite time interval. The uncertainty principle should not be confused with energy conservation - rather it provides mathematical limits to which energy can in principle be defined and measured.
In quantum mechanics energy is expressed using the Hamiltonian operator. On any time scales, the uncertainty in the energy is by
which is similar in form to the Heisenberg uncertainty principle (but not really mathematically equivalent thereto, since H and t are not dynamically conjugate variables, neither in classical nor in quantum mechanics).
In particle physics, this inequality permits a qualitative understanding of virtual particles which carry momentum, exchange by which and with real particles, is responsible for the creation of all known fundamental forces (more accurately known as fundamental interactions). Virtual photons (which are simply lowest quantum mechanical energy state of photons) are also responsible for electrostatic interaction betweenelectric charges (which results in Coulomb law), for spontaneous radiative decay of exited atomic and nuclear states, for the Casimir force, forvan der Waals bond forces and some other observable phenomena.
Applications of the concept of energy
Energy is subject to a strict global conservation law; that is, whenever one measures (or calculates) the total energy of a system of particles whose interactions do not depend explicitly on time, it is found that the total energy of the system always remains constant.[13]
- The total energy of a system can be subdivided and classified in various ways. For example, it is sometimes convenient to distinguishpotential energy (which is a function of coordinates only) from kinetic energy (which is a function of coordinate time derivatives only). It may also be convenient to distinguish gravitational energy, electric energy, thermal energy, and other forms. These classifications overlap; for instance, thermal energy usually consists partly of kinetic and partly of potential energy.
- The transfer of energy can take various forms; familiar examples include work, heat flow, and advection, as discussed below.
- The word "energy" is also used outside of physics in many ways, which can lead to ambiguity and inconsistency. The vernacular terminology is not consistent with technical terminology. For example, while energy is always conserved (in the sense that the total energy does not change despite energy transformations), energy can be converted into a form, e.g., thermal energy, that cannot be utilized to perform work. When one talks about "conserving energy by driving less," one talks about conserving fossil fuels and preventing useful energy from being lost as heat. This usage of "conserve" differs from that of the law of conservation of energy.[11]
In classical physics energy is considered a scalar quantity, the canonical conjugate to time. In special relativity energy is also a scalar (although not a Lorentz scalar but a time component of the energy-momentum 4-vector).[14] In other words, energy is invariant with respect to rotations of space, but not invariant with respect to rotations of space-time (= boosts).
Energy transfer
Because energy is strictly conserved and is also locally conserved (wherever it can be defined), it is important to remember that by the definition of energy the transfer of energy between the "system" and adjacent regions is work. A familiar example is mechanical work. In simple cases this is written as the following equation:
- ΔE = W
(1)
if there are no other energy-transfer processes involved. Here E is the amount of energy transferred, and W represents the work done on the system.
More generally, the energy transfer can be split into two categories:
- ΔE = W + Q
(2)
where Q represents the heat flow into the system.
There are other ways in which an open system can gain or lose energy. In chemical systems, energy can be added to a system by means of adding substances with different chemical potentials, which potentials are then extracted (both of these process are illustrated by fueling an auto, a system which gains in energy thereby, without addition of either work or heat). Winding a clock would be adding energy to a mechanical system. These terms may be added to the above equation, or they can generally be subsumed into a quantity called "energy addition term E" which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses).
- ΔE = W + Q + E
(3)
Where E in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.
Energy is also transferred from potential energy (Ep) to kinetic energy (Ek) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:
- Epi + Eki = EpF + EkF
(4)
The equation can then be simplified further since Ep = mgh (mass times acceleration due to gravity times the height) and 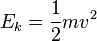 (half mass times velocity squared). Then the total amount of energy can be found by adding Ep + Ek = Etotal.
(half mass times velocity squared). Then the total amount of energy can be found by adding Ep + Ek = Etotal.
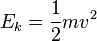 (half mass times velocity squared). Then the total amount of energy can be found by adding Ep + Ek = Etotal.
(half mass times velocity squared). Then the total amount of energy can be found by adding Ep + Ek = Etotal.Energy and the laws of motion
In classical mechanics, energy is a conceptually and mathematically useful property, as it is a conserved quantity. Several formulations of mechanics have been developed using energy as a core concept.
The Hamiltonian
The total energy of a system is sometimes called the Hamiltonian, after William Rowan Hamilton. The classical equations of motion can be written in terms of the Hamiltonian, even for highly complex or abstract systems. These classical equations have remarkably direct analogs in nonrelativistic quantum mechanics.[15]
The Lagrangian
Another energy-related concept is called the Lagrangian, after Joseph Louis Lagrange. This is even more fundamental than the Hamiltonian, and can be used to derive the equations of motion. It was invented in the context of classical mechanics, but is generally useful in modern physics. The Lagrangian is defined as the kinetic energy minus the potential energy.
Usually, the Lagrange formalism is mathematically more convenient than the Hamiltonian for non-conservative systems (such as systems with friction).
Energy and thermodynamics
Internal energy
Internal energy is the sum of all microscopic forms of energy of a system. It is the energy needed to create the system. It is related to the potential energy, e.g., molecular structure, crystal structure, and other geometric aspects, as well as the motion of the particles, in form of kinetic energy. Thermodynamics is chiefly concerned with changes in internal energy and not its absolute value, which is impossible to determine with thermodynamics alone.[16]
The laws of thermodynamics
According to the second law of thermodynamics, work can be totally converted into heat, but not vice versa. This is a mathematical consequence of statistical mechanics. The first law of thermodynamics simply asserts that energy is conserved,[17] and that heat is included as a form of energy transfer. A commonly used corollary of the first law is that for a "system" subject only to pressure forces and heat transfer (e.g., a cylinder-full of gas), the differential change in energy of the system (with a gain in energy signified by a positive quantity) is given as the following equation:
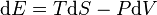 ,
,
where the first term on the right is the heat transfer into the system, defined in terms of temperature T and entropy S (in which entropy increases and the change dS is positive when the system is heated), and the last term on the right hand side is identified as "work" done on the system, where pressure is P and volume V (the negative sign results since compression of the system requires work to be done on it and so the volume change, dV, is negative when work is done on the system). Although this equation is the standard textbook example of energy conservation in classical thermodynamics, it is highly specific, ignoring all chemical, electric, nuclear, and gravitational forces, effects such as advection of any form of energy other than heat, and because it contains a term that depends on temperature. The most general statement of the first law (i.e., conservation of energy) is valid even in situations in which temperature is undefinable.
Energy is sometimes expressed as the following equation:
 ,
,
which is unsatisfactory[11] because there cannot exist any thermodynamic state functions W or Q that are meaningful on the right hand side of this equation, except perhaps in trivial cases.
Equipartition of energy
The energy of a mechanical harmonic oscillator (a mass on a spring) is alternatively kinetic and potential. At two points in the oscillationcycle it is entirely kinetic, and alternatively at two other points it is entirely potential. Over the whole cycle, or over many cycles, net energy is thus equally split between kinetic and potential. This is called equipartition principle; total energy of a system with many degrees of freedom is equally split among all available degrees of freedom.
This principle is vitally important to understanding the behavior of a quantity closely related to energy, called entropy. Entropy is a measure of evenness of a distribution of energy between parts of a system. When an isolated system is given more degrees of freedom (i.e., given new available energy states that are the same as existing states), then total energy spreads over all available degrees equally without distinction between "new" and "old" degrees. This mathematical result is called the second law of thermodynamics.
Oscillators, phonons, and photons
| This section may contain original research. Please improve it by verifying the claims made and adding references. Statements consisting only of original research may be removed. More details may be available on the talk page. (August 2009) |
In an ensemble (connected collection) of unsynchronized oscillators, the average energy is spread equally between kinetic and potential types.
In a solid, thermal energy (often referred to loosely as heat content) can be accurately described by an ensemble of thermal phonons that act as mechanical oscillators. In this model, thermal energy is equally kinetic and potential.
In an ideal gas, the interaction potential between particles is essentially the delta function which stores no energy: thus, all of the thermal energy is kinetic.
Because an electric oscillator (LC circuit) is analogous to a mechanical oscillator, its energy must be, on average, equally kinetic and potential. It is entirely arbitrary whether the magnetic energy is considered kinetic and whether the electric energy is considered potential, or vice versa. That is, either the inductor is analogous to the mass while the capacitor is analogous to the spring, or vice versa.
1. By extension of the previous line of thought, in free space the electromagnetic field can be considered an ensemble of oscillators, meaning that radiation energy can be considered equally potential and kinetic. This model is useful, for example, when the electromagnetic Lagrangianis of primary interest and is interpreted in terms of potential and kinetic energy.
2. On the other hand, in the key equation m2c4 = E2 − p2c2, the contribution mc2 is called the rest energy, and all other contributions to the energy are called kinetic energy. For a particle that has mass, this implies that the kinetic energy is 0.5p2 / m at speeds much smaller thanc, as can be proved by writing E = mc2 √(1 + p2m − 2c − 2) and expanding the square root to lowest order. By this line of reasoning, the energy of a photon is entirely kinetic, because the photon is massless and has no rest energy. This expression is useful, for example, when the energy-versus-momentum relationship is of primary interest.
The two analyses are entirely consistent. The electric and magnetic degrees of freedom in item 1 are transverse to the direction of motion, while the speed in item 2 is along the direction of motion. For non-relativistic particles these two notions of potential versus kinetic energy are numerically equal, so the ambiguity is harmless, but not so for relativistic particles.
Work and virtual work
Work, a form of energy, is force times distance.
This says that the work (W) is equal to the line integral of the force F along a path C; for details see the mechanical work article.
Work and thus energy is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.
Quantum mechanics
Main article: Energy operator
In quantum mechanics energy is defined in terms of the energy operator as a time derivative of the wave function. The Schrödinger equationequates the energy operator to the full energy of a particle or a system. In results can be considered as a definition of measurement of energy in quantum mechanics. The Schrödinger equation describes the space- and time-dependence of slow changing (non-relativistic) wave functionof quantum systems. The solution of this equation for bound system is discrete (a set of permitted states, each characterized by an energy level) which results in the concept of quanta. In the solution of the Schrödinger equation for any oscillator (vibrator) and for electromagnetic waves in a vacuum, the resulting energy states are related to the frequency by the Planck equation E = hν (where h is the Planck's constantand ν the frequency). In the case of electromagnetic wave these energy states are called quanta of light or photons.
Relativity
When calculating kinetic energy (work to accelerate a mass from zero speed to some finite speed) relativistically - using Lorentz transformations instead of Newtonian mechanics, Einstein discovered an unexpected by-product of these calculations to be an energy term which does not vanish at zero speed. He called it rest mass energy - energy which every mass must possess even when being at rest. The amount of energy is directly proportional to the mass of body:
- E = mc2,
where
- m is the mass,
- c is the speed of light in vacuum,
- E is the rest mass energy.
For example, consider electron-positron annihilation, in which the rest mass of individual particles is destroyed, but the inertia equivalent of the system of the two particles (its invariant mass) remains (since all energy is associated with mass), and this inertia and invariant mass is carried off by photons which individually are massless, but as a system retain their mass. This is a reversible process - the inverse process is called pair creation - in which the rest mass of particles is created from energy of two (or more) annihilating photons. In this system thematter (electrons and positrons) is destroyed and changed to non-matter energy (the photons). However, the total system mass and energy do not change during this interaction.
In general relativity, the stress-energy tensor serves as the source term for the gravitational field, in rough analogy to the way mass serves as the source term in the non-relativistic Newtonian approximation.[14]
It is not uncommon to hear that energy is "equivalent" to mass. It would be more accurate to state that every energy has an inertia and gravity equivalent, and because mass is a form of energy, then mass too has inertia and gravity associated with it.
Energy and life
Main article: Bioenergetics

Basic overview of energy and human life.
Any living organism relies on an external source of energy—radiation from the Sun in the case of green plants; chemical energy in some form in the case of animals—to be able to grow and reproduce. The daily 1500–2000 Calories (6–8 MJ) recommended for a human adult are taken as a combination of oxygen and food molecules, the latter mostly carbohydrates and fats, of whichglucose (C6H12O6) and stearin (C57H110O6) are convenient examples. The food molecules are oxidised to carbon dioxide and water in the mitochondria
-
- C6H12O6 + 6O2 → 6CO2 + 6H2O
- C57H110O6 + 81.5O2 → 57CO2 + 55H2O
-
- ADP + HPO42− → ATP + H2O
The rest of the chemical energy in the carbohydrate or fat is converted into heat: the ATP is used as a sort of "energy currency", and some of the chemical energy it contains when split and reacted with water, is used for other metabolism(at each stage of a metabolic pathway, some chemical energy is converted into heat). Only a tiny fraction of the original chemical energy is used for work:[18]
- gain in kinetic energy of a sprinter during a 100 m race: 4 kJ
- gain in gravitational potential energy of a 150 kg weight lifted through 2 metres: 3kJ
- Daily food intake of a normal adult: 6–8 MJ
It would appear that living organisms are remarkably inefficient (in the physical sense) in their use of the energy they receive (chemical energy or radiation), and it is true that most real machines manage higher efficiencies. In growing organisms the energy that is converted to heat serves a vital purpose, as it allows the organism tissue to be highly ordered with regard to the molecules it is built from. The second law of thermodynamics states that energy (and matter) tends to become more evenly spread out across the universe: to concentrate energy (or matter) in one specific place, it is necessary to spread out a greater amount of energy (as heat) across the remainder of the universe ("the surroundings").[19] Simpler organisms can achieve higher energy efficiencies than more complex ones, but the complex organisms can occupy ecological niches that are not available to their simpler brethren. The conversion of a portion of the chemical energy to heat at each step in a metabolic pathway is the physical reason behind the pyramid of biomass observed in ecology: to take just the first step in the food chain, of the estimated 124.7 Pg/a of carbon that is fixed by photosynthesis, 64.3 Pg/a (52%) are used for the metabolism of green plants,[20]i.e. reconverted into carbon dioxide and heat.
Measurement
Because energy is defined as the ability to do work on objects, there is no absolute measure of energy. Only the transition of a system from one state into another can be defined and thus energy is measured in relative terms. The choice of a baseline or zero point is often arbitrary and can be made in whatever way is most convenient for a problem.
Methods
The methods for the measurement of energy often deploy methods for the measurement of still more fundamental concepts of science, namely mass, distance, radiation, temperature, time,electric charge and electric current.
Conventionally the technique most often employed is calorimetry, a thermodynamic technique that relies on the measurement of temperature using a thermometer or of intensity of radiation using abolometer.
Units
Main article: Units of energy
Throughout the history of science, energy has been expressed in several different units such as ergs and calories. At present, the accepted unit of measurement for energy is the SI unit of energy, the joule. In addition to the joule, other units of energy include the kilowatt hour (kWh) and the British thermal unit (Btu). These are both larger units of energy. One kWh is equivalent to exactly 3.6 million joules, and one Btu is equivalent to about 1055 joules.[21]
Energy density
Main article: Energy density
Energy density is a term used for the amount of useful energy stored in a given system or region of space per unit volume.
For fuels, the energy per unit volume is sometimes a useful parameter. In a few applications, comparing, for example, the effectiveness ofhydrogen fuel to gasoline it turns out that hydrogen has a higher specific energy than does gasoline, but, even in liquid form, a much lower energy density.
Forms of energy
In the context of physical sciences, several forms of energy have been defined. These include:
|
These energies may be divided into two main groups; kinetic energy and potential energy. Other familiar types of energy are a varying mix of both potential and kinetic energy. Energy may betransformed between these forms.
The above list of the known possible forms of energy is not necessarily complete. Whenever physical scientists discover that a certain phenomenon appears to violate the law of energy conservation, new forms may be added, as is the case with dark energy, a hypothetical form of energy that permeates all of space and tends to increase the rate of expansion of the universe.
Classical mechanics distinguishes between potential energy, which is a function of the position of an object, and kinetic energy, which is a function of its movement. Both position and movement are relative to a frame of reference, which must be specified: this is often (and originally) an arbitrary fixed point on the surface of the Earth, the terrestrial frame of reference. It has been attempted to categorize all forms of energy as either kinetic or potential: this is not incorrect, but neither is it clear that it is a real simplification, as Feynman points out:
These notions of potential and kinetic energy depend on a notion of length scale. For example, one can speak of macroscopicpotential and kinetic energy, which do not include thermal potential and kinetic energy. Also what is called chemical potential energy (below) is a macroscopic notion, and closer examination shows that it is really the sum of the potential and kinetic energy on the atomic and subatomic scale. Similar remarks apply to nuclear "potential" energy and most other forms of energy. This dependence on length scale is non-problematic if the various length scales are decoupled, as is often the case ... but confusion can arise when different length scales are coupled, for instance when friction converts macroscopic work into microscopic thermal energy.
| Mechanical energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Lever |
| Thermal energy | Brakes |
| Electric energy | Dynamo |
| Electromagnetic radiation | Synchrotron |
| Chemical energy | Matches |
| Nuclear energy | Particle accelerator |
Mechanical energy
Mechanical energy manifest in many forms,but can be broadly classified into elastic potential energy and kinetic energy. The term potential energy is a very general term, because it exists in all force fields, such as gravitation, electrostatic and magnetic fields. Potential energy refers to the energy any object gets due to its position in a force field.
Main article: Potential energy
Potential energy, symbols Ep, V or Φ, is defined as the work done against a given force (= work of given force with minus sign) in changing the position of an object with respect to a reference position (often taken to be infinite separation). If F is the force and s is the displacement,
with the dot representing the scalar product of the two vectors.
The name "potential" energy originally signified the idea that the energy could readily be transferred as work—at least in an idealized system (reversible process, see below). This is not completely true for any real system, but is often a reasonable first approximation in classical mechanics.
The general equation above can be simplified in a number of common cases, notably when dealing withgravity or with elastic forces.
Elastic potential energy

As a ball falls freely under the influence of gravity, it accelerates downward, its initial potential energy converting into kinetic energy. On impact with a hard surface the ball deforms, converting the kinetic energy into elastic potential energy. As the ball springs back, the energy converts back firstly to kinetic energy and then as the ball re-gains height into potential energy. Energy conversion to heat due to inelasticdeformation and air resistance cause each successive bounce to be lower than the last.
Main article: Elastic potential energy
Elastic potential energy is defined as a work needed to compress (or expand) a spring. The force,F, in a spring or any other system which obeys Hooke's law is proportional to the extension or compression, x,
-
- F = − kx
where k is the force constant of the particular spring (or system). In this case, the calculated work becomes
only when k is constant. Hooke's law is a good approximation for behaviour of chemical bondsunder normal conditions, i.e. when they are not being broken or formed.
Kinetic energy
Main article: Kinetic energy
Kinetic energy, symbols Ek, T or K, is the work required to accelerate an object to a given speed. Indeed, calculating this work one easily obtains the following:
At speeds approaching the speed of light, c, this work must be calculated using Lorentz transformations, which results in the following:
Here the two terms on the right hand side are identified with the total energy and the rest energy of the object, respectively. This equation reduces to the one above it, at small (compared to c) speed. The kinetic energy is zero at v=0, so that at rest, the total energy is the rest energy. Thus, a resting mass has the amount of total energy equal to:
-
- Erest = mc2
This energy is thus called rest mass energy.
Surface energy
If there is any kind of tension in a surface, such as a stretched sheet of rubber or material interfaces, it is possible to define surface energy. In particular, any meeting of dissimilar materials that don't mix will result in some kind of surface tension, if there is freedom for the surfaces to move then, as seen in capillary surfaces for example, the minimum energy will as usual be sought.
A minimal surface, for example, represents the smallest possible energy that a surface can have if its energy is proportional to the area of the surface. For this reason, (open) soap films of small size are minimal surfaces (small size reduces gravity effects, and openness prevents pressure from building up. Note that a bubble is a minimum energy surface but not a minimal surface by definition).
Sound energy
Sound is a form of mechanical vibration which propagates through any mechanical medium. It is closely related to the ability of the human ear to perceive sound. The wide outer area of the ear is maximized to collect sound vibrations. It is amplified and passed through the outer ear, striking the eardrum, which transmits sounds into the inner ear. Auditory nerves fire according to the particular vibrations of the sound waves in the inner ear, which designate such things as the pitch and volume of the sound. The ear is set up in an optimal way to interpret sound energy in the form of vibrations.
Gravitational energy
Main article: Gravitational potential energy
The gravitational force near the Earth's surface varies very little with the height, h, and is equal to the mass, m, multiplied by the gravitational acceleration, g = 9.81 m/s². In these cases, the gravitational potential energy is given by
-
- Ep,g = mgh
A more general expression for the potential energy due to Newtonian gravitation between two bodies of masses m1 and m2, useful inastronomy, is
-
 ,
,
where r is the separation between the two bodies and G is the gravitational constant, 6.6742(10)×10−11 m3kg−1s−2.[22] In this case, the reference point is the infinite separation of the two bodies.
Thermal energy
| Thermal energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Steam turbine |
| Thermal energy | Heat exchanger |
| Electric energy | Thermocouple |
| Electromagnetic radiation | Hot objects |
| Chemical energy | Blast furnace |
| Nuclear energy | Supernova |
Main article: Thermal energy
Thermal energy (of some media - gas, plasma, solid, etc.) is the energy associated with the microscopical random motion of particles constituting the media. For example, in case of monoatomic gas it is just a kinetic energy of motion of atoms of gas as measured in the reference frame of the center of mass of gas. In case of molecules in the gas rotational and vibrational energy is involved. In the case of liquids and solids there is also potential energy (of interaction of atoms) involved, and so on.
A heat is defined as a transfer (flow) of thermal energy across certain boundary (for example, from a hot body to cold via the area of their contact. A practical definition for small transfers of heat is
where Cv is the heat capacity of the system. This definition will fail if the system undergoes a phase transition—e.g. if ice is melting to water—as in these cases the system can absorb heat without increasing its temperature. In more complex systems, it is preferable to use the concept of internal energy rather than that of thermal energy (see Chemical energy below).
Despite the theoretical problems, the above definition is useful in the experimental measurement of energy changes. In a wide variety of situations, it is possible to use the energy released by a system to raise the temperature of another object, e.g. a bath of water. It is also possible to measure the amount of electric energy required to raise the temperature of the object by the same amount. The calorie was originally defined as the amount of energy required to raise the temperature of one gram of water by 1 °C (approximately 4.1855 J, although the definition later changed), and the British thermal unit was defined as the energy required to heat one pound of water by 1 °F (later fixed as 1055.06 J).
Electric energy
Main articles: Electromagnetism and Electricity
| Electric energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Electric motor |
| Thermal energy | Resistor |
| Electric energy | Transformer |
| Electromagnetic radiation | Light-emitting diode |
| Chemical energy | Electrolysis |
| Nuclear energy | Synchrotron |
Electrostatic energy
The electric potential energy of given configuration of charges is defined as the work which must be done against the Coulomb force to rearrange charges from infinite separation to this configuration (or the work done by the Coulomb force separating the charges from this configuration to infinity). For two point-like charges Q1 and Q2 at a distance r this work, and hence electric potential energy is equal to:
where ε0 is the electric constant of a vacuum, 107/4πc0² or 8.854188…×10−12 F/m.[22] If the charge is accumulated in a capacitor (of capacitance C), the reference configuration is usually selected not to be infinite separation of charges, but vice versa - charges at an extremely close proximity to each other (so there is zero net charge on each plate of a capacitor). The justification for this choice is purely practical - it is easier to measure both voltage difference and magnitude of charges on a capacitor plates not versus infinite separation of charges but rather versus discharged capacitor where charges return to close proximity to each other (electrons and ions recombine making the plates neutral). In this case the work and thus the electric potential energy becomes
Electric energy
If an electric current passes through a resistor, electric energy is converted to heat; if the current passes through an electric appliance, some of the electric energy will be converted into other forms of energy (although some will always be lost as heat). The amount of electric energy due to an electric current can be expressed in a number of different ways:
where U is the electric potential difference (in volts), Q is the charge (in coulombs), I is the current (in amperes), t is the time for which the current flows (in seconds), P is the power (in watts) and R is the electric resistance (in ohms). The last of these expressions is important in the practical measurement of energy, as potential difference, resistance and time can all be measured with considerable accuracy.
Magnetic energy
There is no fundamental difference between magnetic energy and electric energy: the two phenomena are related by Maxwell's equations. The potential energy of a magnet of magnetic moment m in a magnetic field B is defined as the work of magnetic force (actually of magnetictorque) on re-alignment of the vector of the magnetic dipole moment, and is equal:
while the energy stored in an inductor (of inductance L) when current I is passing via it is
-
 .
.
This second expression forms the basis for superconducting magnetic energy storage.
Electromagnetic Energy
| Electromagnetic radiation is converted | |
|---|---|
| into | by |
| Mechanical energy | Solar sail |
| Thermal energy | Solar collector |
| Electric energy | Solar cell |
| Electromagnetic radiation | Non-linear optics |
| Chemical energy | Photosynthesis |
| Nuclear energy | Mössbauer spectroscopy |
Calculating work needed to create an electric or magnetic field in unit volume (say, in a capacitor or an inductor) results in the electric and magnetic fields energy densities:
and
-
 ,
,
in SI units.
Electromagnetic radiation, such as microwaves, visible light or gamma rays, represents a flow of electromagnetic energy. Applying the above expressions to magnetic and electric components of electromagnetic field both the volumetric density and the flow of energy in e/m field can be calculated. The resulting Poynting vector, which is expressed as
in SI units, gives the density of the flow of energy and its direction.
The energy of electromagnetic radiation is quantized (has discrete energy levels). The spacing between these levels is equal to
-
- E = hν
where h is the Planck constant, 6.6260693(11)×10−34 Js,[22] and ν is the frequency of the radiation. This quantity of electromagnetic energy is usually called a photon. The photons which make up visible light have energies of 270–520 yJ, equivalent to 160–310 kJ/mol, the strength of weaker chemical bonds.
Chemical energy
Main article: Chemical thermodynamics
| Chemical energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Muscle |
| Thermal energy | Fire |
| Electric energy | Fuel cell |
| Electromagnetic radiation | Glowworms |
| Chemical energy | Chemical reaction |
Chemical energy is the energy due to associations of atoms in molecules and various other kinds of aggregates of matter. It may be defined as a work done by electric forces during re-arrangement of mutual positions of electric charges, electrons and protons, in the process of aggregation. So, basically it is electrostatic potential energy of electric charges. If the chemical energy of a system decreases during a chemical reaction, the difference is transferred to the surroundings in some form (often heat or light); on the other hand if the chemical energy of a system increases as a result of a chemical reaction - the difference then is supplied by the surroundings (usually again in form of heat or light). For example,
- when two hydrogen atoms react to form a dihydrogen molecule, the chemical energy decreases by 724 zJ (the bond energy of the H–H bond);
- when the electron is completely removed from a hydrogen atom, forming a hydrogen ion (in the gas phase), the chemical energy increases by 2.18 aJ (the ionization energy of hydrogen).
It is common to quote the changes in chemical energy for one mole of the substance in question: typical values for the change in molar chemical energy during a chemical reaction range from tens to hundreds of kilojoules per mole.
The chemical energy as defined above is also referred to by chemists as the internal energy, U: technically, this is measured by keeping the volume of the system constant. Most practical chemistry is performed at constant pressure and, if the volume changes during the reaction (e.g. a gas is given off), a correction must be applied to take account of the work done by or on the atmosphere to obtain the enthalpy, H:
-
- ΔH = ΔU + PΔV
A second correction, for the change in entropy, S, must also be performed to determine whether a chemical reaction will take place or not, giving the Gibbs free energy, G:
-
- ΔG = ΔH − TΔS
These corrections are sometimes negligible, but often not (especially in reactions involving gases).
Since the industrial revolution, the burning of coal, oil, natural gas or products derived from them has been a socially significant transformation of chemical energy into other forms of energy. the energy "consumption" (one should really speak of "energy transformation") of a society or country is often quoted in reference to the average energy released by the combustion of these fossil fuels:
- 1 tonne of coal equivalent (TCE) = 29.3076 GJ = 8,141 kilowatt hour
- 1 tonne of oil equivalent (TOE) = 41.868 GJ = 11,630 kilowatt hour
On the same basis, a tank-full of gasoline (45 litres, 12 gallons) is equivalent to about 1.6 GJ of chemical energy. Another chemically based unit of measurement for energy is the "tonne of TNT", taken as 4.184 GJ. Hence, burning a tonne of oil releases about ten times as much energy as the explosion of one tonne of TNT: fortunately, the energy is usually released in a slower, more controlled manner.
Simple examples of storage of chemical energy are batteries and food. When food is digested and metabolized (often with oxygen), chemical energy is released, which can in turn be transformed into heat, or by muscles into kinetic energy.
Nuclear energy
Main article: Nuclear binding energy
| Nuclear binding energy is converted | |
|---|---|
| into | by |
| Mechanical energy | Alpha radiation |
| Thermal energy | Sun |
| Electrical energy | Beta radiation |
| Electromagnetic radiation | Gamma radiation |
| Chemical energy | Radioactive decay |
| Nuclear energy | Nuclear isomerism |
Nuclear potential energy, along with electric potential energy, provides the energy released from nuclear fission and nuclear fusion processes. The result of both these processes are nuclei in which the more-optimal size of the nucleus allows the nuclear force (which is opposed by the electromagnetic force) to bind nuclear particles more tightly together than before the reaction.
The Weak nuclear force (different from the strong force) provides the potential energy for certain kinds of radioactive decay, such as beta decay.
The energy released in nuclear processes is so large that the relativistic change in mass (after the energy has been removed) can be as much as several parts per thousand.
Nuclear particles (nucleons) like protons and neutrons are not destroyed (law of conservation of baryon number) in fission and fusion processes. A few lighter particles may be created or destroyed (example: beta minus and beta plus decay, or electron capture decay), but these minor processes are not important to the immediate energy release in fission and fusion. Rather, fission and fusion release energy when collections of baryons become more tightly bound, and it is the energy associated with a fraction of the mass of the nucleons (but not the whole particles) which appears as the heat and electromagnetic radiation generated by nuclear reactions. This heat and radiation retains the "missing" mass, but the mass is missing only because it escapes in the form of heat or light, which retain the mass and conduct it out of the system where it is not measured.
The energy from the Sun, also called solar energy, is an example of this form of energy conversion. In theSun, the process of hydrogen fusion converts about 4 million metric tons of solar matter per second into light, which is radiated into space, but during this process, the number of total protons and neutrons in the sun does not change. In this system, the light itself retains the inertial equivalent of this mass, and indeed the mass itself (as a system), which represents 4 million tons per second of electromagnetic radiation, moving into space. Each of the helium nuclei which are formed in the process are less massive than the four protons from they were formed, but (to a good approximation), no particles or atoms are destroyed in the process of turning the sun's nuclear potential energy into light.
Transformations of energy
Main article: Energy conversion
One form of energy can often be readily transformed into another with the help of a device- for instance, a battery, from chemical energy toelectric energy; a dam: gravitational potential energy to kinetic energy of moving water (and the blades of a turbine) and ultimately to electric energy through an electric generator. Similarly, in the case of a chemical explosion, chemical potential energy is transformed to kinetic energy and thermal energy in a very short time. Yet another example is that of a pendulum. At its highest points the kinetic energy is zero and the gravitational potential energy is at maximum. At its lowest point the kinetic energy is at maximum and is equal to the decrease ofpotential energy. If one (unrealistically) assumes that there is no friction, the conversion of energy between these processes is perfect, and the pendulum will continue swinging forever.
Energy gives rise to weight when it is trapped in a system with zero momentum, where it can be weighed. It is also equivalent to mass, and this mass is always associated with it. Mass is also equivalent to a certain amount of energy, and likewise always appears associated with it, as described in mass-energy equivalence. The formula E = mc², derived by Albert Einstein (1905) quantifies the relationship between rest-mass and rest-energy within the concept of special relativity. In different theoretical frameworks, similar formulas were derived by J. J. Thomson (1881), Henri Poincaré (1900), Friedrich Hasenöhrl (1904) and others (see Mass-energy equivalence#History for further information).
Matter may be destroyed and converted to energy (and vice versa), but mass cannot ever be destroyed; rather, mass remains a constant for both the matter and the energy, during any process when they are converted into each other. However, since c2 is extremely large relative to ordinary human scales, the conversion of ordinary amount of matter (for example, 1 kg) to other forms of energy (such as heat, light, and other radiation) can liberate tremendous amounts of energy (~9x1016 joules = 21 megatons of TNT), as can be seen in nuclear reactors and nuclear weapons. Conversely, the mass equivalent of a unit of energy is minuscule, which is why a loss of energy (loss of mass) from most systems is difficult to measure by weight, unless the energy loss is very large. Examples of energy transformation into matter (i.e., kinetic energy into particles with rest mass) are found in high-energy nuclear physics.
Transformation of energy into useful work is a core topic of thermodynamics. In nature, transformations of energy can be fundamentally classed into two kinds: those that are thermodynamically reversible, and those that are thermodynamically irreversible. A reversible process in thermodynamics is one in which no energy is dissipated (spread) into empty energy states available in a volume, from which it cannot be recovered into more concentrated forms (fewer quantum states), without degradation of even more energy. A reversible process is one in which this sort of dissipation does not happen. For example, conversion of energy from one type of potential field to another, is reversible, as in the pendulum system described above. In processes where heat is generated, quantum states of lower energy, present as possible exitations in fields between atoms, act as a reservoir for part of the energy, from which it cannot be recovered, in order to be converted with 100% efficiency into other forms of energy. In this case, the energy must partly stay as heat, and cannot be completely recovered as usable energy, except at the price of an increase in some other kind of heat-like increase in disorder in quantum states, in the universe (such as an expansion of matter, or a randomization in a crystal).
As the universe evolves in time, more and more of its energy becomes trapped in irreversible states (i.e., as heat or other kinds of increases in disorder). This has been referred to as the inevitable thermodynamic heat death of the universe. In this heat death the energy of the universe does not change, but the fraction of energy which is available to do produce work through a heat engine, or be transformed to other usable forms of energy (through the use of generators attached to heat engines), grows less and less.
Subscribe to:
Comments (Atom)